Locos por la Geología

Figura 1. elipse.

Este post es la continuación del que subí el lunes pasado, que me resultó³ un poco extenso porque, como me pasa siempre, me entusiasmé demasiado escribiendo. 😀 .

Las preguntas que allí respondí son las siguientes:

¿Quién era Kepler y cuándo formuló sus leyes?

¿Cuántas son y a qué se refieren las leyes de Kepler?

¿Qué dice la primera ley de Kepler?

Y hoy retomamos desde allí.

¿Qué es una elipse?

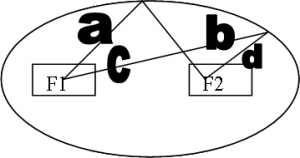
Es el lugar geométrico de todos los puntos para los cuales la suma de las distancias a dos puntos fijos, llamados focos, es constante. (Vean la Figura 1).

Esto se puede decir más fácil a través de una fó³rmula, aunque no lo crean, y es la siguiente:

a+b=c+d

En otras palabras, no importa dónde se paren ustedes a lo largo de la figura de una elipse, siempre la distancia desde ese punto al foco f1, más la distancia desde ese mismo punto al foco f2, será exactamente la misma, vale decir, que permanece «constantemente constante». 😀 .

Respecto a la otra palabreja, la excentricidad, se refiere a la medida de la desviación respecto a la circunferencia en que mejor se inscribe. Cuanto más se aproxima la relación entre ambos perímetros a 1, más parecida al círculo es la elipse correspondiente. Cuando se dice que las órbitas de los planetas son poco excéntricas, se está diciendo que no son excesivamente alargadas, como lo son, por ejemplo, las de los cometas.

¿Qué dice la segunda ley de Kepler?

El radiovector que une el sol con el planeta, recorre áreas iguales en tiempos iguales. Para esto, cada planeta se desplaza con mayor velocidad en la porción de su órbita más cercana al Sol. (Figura 2)

Para entender mejor la figura, les aclaro que en cada caso, el segmento entre los puntos a, b,c, y d, y el sol, está representando distintas posiciones del radiovector a lo largo de la órbita del planeta. O sea, marca el mismo radiovector, que se va desplazando. Y el planeta aparece dibujado dos veces, porque se trata de dos momentos distintos de su recorrido, pero obviamente es único.

En dos momentos diferentes, el área barrida por ese radiovector está representada por los triángulos circulares marcados como E y F. Y si ustedes se fijan, uno es más largo y flaco, y el otro más cortito y ancho, con lo cual (aunque el dibujo no está hecho a escala) E y F pueden considerarse áreas iguales.

Ahora bien, si esas dos áreas iguales (E y F) se barren en tiempos iguales, surge una consecuencia importante, que veremos ahora.

Fíjense no ya en el área sino en el borde solamente, es decir en la propia trayectoria del planeta. Entre a y b hay más distancia que entre c y d.

Pero la velocidad es igual al espacio sobre el tiempo, y si el tiempo no cambia, pero el espacio crece, necesariamente la  velocidad ha de aumentar en a-b, que es casualmente cuando el planeta está más próximo al Sol.

Digámoslo de otra forma, si me mandan a caminar entre la plaza y mi casa, distante diez cuadras, en dos horas, y después me dicen que en el mismo tiempo tengo que ir, en cambio, hasta el límite de la Provincia- a cientos de kilómetros de distancia-, sucederán dos cosas:

1. tendré que correr mucho más rápido y
2. lo mismo no voy a llegar ni a palos.

Pero, concéntrense en la situación 1 que es la que quería demostrar.

¿Qué explicación tiene este fenómeno?

Actualmente, esto puede explicarse en términos de energía. En una órbita elíptica, donde la distancia entre el cuerpo central y el que se mueve a su alrededor no es constante, la energía gravitacional requerida por el sistema disminuye cuando el cuerpo orbitante se acerca al central. En ese momento, la energía gravitacional excedente se transforma en energía cinética, que acelera al cuerpo. Inversamente, al alejarse la masa externa de la central, la energía cinética se transforma en gravitacional, perdiéndose así velocidad.

Esto se repite cíclicamente, y es resultante de la ley de la Gravedad que ya les expliqué en otro post.

Para su tranquilidad, lo puedo explicar más fácil. Si estoy corriendo alrededor de la calesita en movimiento, tomada del borde, es mejor que me agarre con las dos manos y estaré ocupando demasiada energía en no soltarme como para poder correr a mucha velocidad, pero si en cambio estoy asegurada a ella, digamos por un soporte rígido que me asegura que no saldré despedida, me quedará resto para correr mucho más rápido. Por las dudas no hagan la prueba, me alcanza con que entiendan el punto que quiero demostrar.

¿Qué dice la tercera ley de Kepler?

Los cuadrados de los tiempos de las revoluciones son proporcionales a los cubos de las distancias medias de los planetas respecto al Sol.

Esta ley se relaciona conceptualmente con la anterior, más lejos, menos velocidad.

Pero en este caso estoy hablando no ya del mismo planeta a lo largo de su recorrido, sino que estoy relacionando los planetas unos con otros, y viendo la proporcionalidad que existe entre sus posiciones y velocidades.

¿Cuál es la importancia de estas leyes?

Pues ellas permiten predecir y comprender todos los movimientos planetarios. Y por otra parte, señalan el pasaje desde lo que era antes una mezcla de ciencia, mitos, creencias, astrología mágica y especulaciones, a una astromía fundamentada en hechos explicables de modo racional.

Un abrazo y hasta el miércoles. Graciela

Este post lo he construido sobre la base de un apunte de mi propia autoría que se identifica como sigue:

Argüello, Graciela L. 2006.» La Tierra como planeta integrante del Sistema Solar» Cuadernillo didáctico Nº II, Capítulo 1. Para circulación interna en la U.N.R.C. 17 páginas.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque está registrado con IBSN N° 04-10-1952-01.