Locos por la Geología

Ya hemos hablado de varios temas relativos a la dinámica fluvial, y es un buen momento para explicar algunos principios físico- matemáticos que rigen el transporte y la sedimentación de las partículas transportadas por un fluido en movimiento.

Y digo un fluido y no el agua, porque son igualmente válidos para el movimiento del aire, es decir el viento, cambiando solamente algunos valores numéricos en los ejes X e Y.

Lo que les presento entonces hoy es la Curva de Hjulström, que complementaré más tarde con la ley de Stokes, en otro post.

¿Quién fue Hjulström?

Filip Hjulström nació en Suecia el 6 de octubre de 1902, y se hizo mundialmente conocido por la publicación de su tesis doctoral titulada «The River Fyris» (el Río Fyris), en la que presentó uno de los primeros estudios cuantitativos sobre procesos geomorfológicos de que se guarda registro.

Posteriormente, en conjunto con sus alumnos, continuó estudios de tal importancia, que llegaron a constituir la Escuela Upsala de Geografía Física. Hjulström falleció en 1982, dejando un importante legado científico, y sin haberlo sospechado nunca, también artístico.

En efecto (y esto lo agrego como nota de color), Filip Hjulström, fue el padre de Lennart Hjulström, que se convertiría en un notable actor sueco, casado con la también actriz Ulla Söderdal, con quien tendría dos hijos que también se dedicaron a la actuación: Niklas y Carin Hjulström.

¿Qué es la curva de Hjulström?

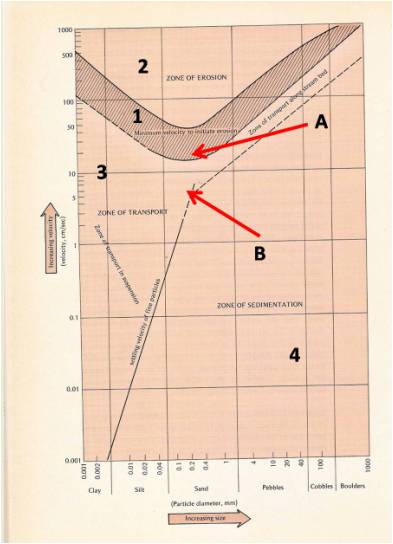
La curva de Hjulström es un diagrama de uso muy extendido en la Geomorfología, que describe los umbrales que en función de los cambios de velocidad de una corriente, definen si hay arranque, transporte o sedimentación. para cada tamaño de partícula involucrada en el proceso.

¿Cómo se entiende la curva de Hjulström?

Como siempre he dicho a mis alumnos, para comprender un diagrama cualquiera, lo primero a hacer es observarlo. Ver en detalle qué partes lo conforman, qué unidades de medida están involucradas, y cómo se comportan las curvas, barras o campos resultantes. Hagámoslo así, pues.

¿Qué rasgos se destacan en la curva?

Se trata de un sistema de ejes XY, compuesto por los siguientes elementos:

• En el eje X (abcisas), se observan los diversos tamaños de partículas presentes en el curso del río en este caso, aunque podría aplicarse (cambiando sólo los valores aritméticos) a fenómenos eólicos, es decir corrientes de aire. Sobre las abcisas, los tamaños crecen desde la intersección de los dos ejes, hacia la derecha, y se miden en mm. Allí aparecen intervalos de tamaños que corresponden sucesivamente a las arcillas, limos, arenas, guijas, guijarros y guijones.
• El eje Y (ordenadas) implica el crecimiento hacia arriba de la velocidad del fluido en movimiento, y la unidad es m/segundo.
• Ya en el interior del diagrama, se observan las curvas que conectan todos los puntos críticos en que las partículas de cada tamaño, pasan de una situación a otra diferente, ya sea de reposo a arranque, de arranque a transporte o de transporte a sedimentación. En un caso se trata de curvas literalmente, y en otro caso se trata de dos segmentos rectos, que de todos modos se designan como curva.
• Esas curvas que mencionamos arriba, separan distintos campos, a saber: zona de erosión (propiamente dicha, o arranque del material), que les he marcado con un 2 en el gráfico; zona de transporte, que marqué con 3; y la zona 4, que es la de sedimentación o depósito. La zona 2 o de arranque, está en la porción más alta del gráfico porque es la que requiere mayor velocidad. Una vez puesta en movimiento la partícula, la energía necesaria para mantenerla en tránsito puede ser menor, porque la propia inercia juega a su favor.
• La zona que les indiqué con 1, es un intervalo que incluye las velocidades mínimas que se requieren para que los materiales de cada tamaño sean arrancados del cauce, sea del lecho o de las riberas. Es una zona y no una sola línea, porque hay numerosos factores que la afectan, como por ejemplo, la turbulencia, la carga que ya transporta el agua y que modifica su potencia neta, etc.
• Por arriba del punto B, la zona de transporte implica un arrastre de materiales gruesos por el fondo del lecho, mientras que hacia abajo de ese punto, siendo menor la velocidad, se transportan partículas finas por otros mecanismos, como flotación, rodamiento, saltación, y más abajo aún, (es decir con menos velocidad) por suspensión.

¿Por qué desciende la curva en el punto A?

Figura 1. La cohesión de las arcillas.

La lógica indica que cuanto más pequeña es la partícula, menor es la velocidad requerida para el arranque y puesta en movimiento.

Esto nos haría pensar que la curva debería ser siempre ascendente hacia la derecha donde se encuentran los tamaños más gruesos, y sin embargo, hay una menor velocidad crítica en ese punto A, que corresponde al tamaño de los limos.

Eso ocurre porque las partículas más finas que el limo, tienen una fuerza de cohesión que debe ser vencida para el arranque, que no aparece en cambio en el limo y las demás partículas. Por eso, en el extremo de la izquierda, donde están las partículas de arcilla, se necesita más velocidad para la erosión ss, y la curva sube.

La explicación está en la característica micelar de las arcillas que por diversas razones, tienen normalmente carga eléctrica negativa en sus bordes (Figura 1). Al estar inmersas las partículas en agua, o en presencia de humedad, las propias moléculas de agua- con sus cargas orientadas que constituyen dipolos eléctricos– actúan como aglutinantes de las micelas de arcilla, al unir sus cargas positivas a los polos negativos de estas últimas.

¿Por qué cambia bruscamente la pendiente de la curva en el punto B?

Porque hacia la derecha, el tamaño tan grande de los materiales involucrados, requiere una gran energía para el transporte, y un mínimo descenso en la velocidad del flujo pasa los cuerpos transportados de ese campo, al de la sedimentación, en otras palabras, se depositan rápidamente.

Traducido: para una amplio rango de tamaños, hay ligeros cambios de velocidad crítica para el depósito, por eso, la curva se horizontaliza comparativamente. Hacia la izquierda ocurre exactamente lo inverso. La curva se empina porque se necesitan grandes cambios de velocidad sobre el eje Y, para que los tamaños decrecientes de partículas resulten depositadas, pues muchas de ellas pueden incluso permanecer en suspensión con velocidades próximas al cero.

Pero eso ya lo describe la ley de Stokes que veremos en otro post.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La imagen que ilustra el post es una modificación personal sobre la figura que aparece en el libro The Evolving Earth, de Sawkins.