Locos por la Geología

Al hombre le encanta medir, como si conocer números relacionados con algún objeto material le diera a éste una validación.

Por eso es que desde muchos siglos atrás se vienen haciendo intentos por conocer cada vez con más detalle las diversas medidas del planeta que habitamos, casi como si fuéramos a hacerle un trajecito a medida.

Por supuesto, podemos enumerar una serie de cantidades para referirnos al volumen, diámetro, superficie, etc., etc., de nuestro hogar planetario, y por cierto más abajo les pasaré algunos datos; pero mucho más entretenido es recordar y comprender cómo se fue arribando a ese conocimiento.

Y para empezar, iremos muchos siglos hacia atrás, hasta la primera medición del arco de meridiano, tema no por muy repetido menos apasionante…y a veces mal comprendido.

Como mi experiencia docente me ha demostrado que todos lo han leído, lo repiten y hablan de él, pero no todos podrían explicarlo a su vez, me propongo desarrollarlo pasito a paso, como para que hasta un niño lo entienda cabalmente.

Los que ya lo tienen bien incorporado, pueden salir al recreo, pero antes empecemos por mencionar solamente algunos datos relativos al tamaño de la tierra, y dejemos la historia de esos descubrimientos como tema de otros muchos posts.

¿Cuáles son las dimensiones más significativas de la Tierra?

Convengamos para empezar que se trata de medidas permanentemente sujetas a revisión, y que se van corrigiendo a medida que se inventan aparatos y tecnologías cada vez más precisas y exactas, de modo que las que aquí incluyo son básicamente para que nos ubiquemos en un rango realista, a la hora de imaginar este enorme hogar que nos cobija.

También es importante recordar que la verdadera forma de la Tierra es el geoide (que ya les expliqué en otro post), y que por ese motivo las expresiones «diámetro polar» o «diámetro ecuatorial», deben ser tomadas como meras aproximaciones a una realidad que no representan de modo absoluto.

Hechas estas salvedades, les paso los datos más relevantes:

Diámetro Ecuatorial: 12.756 Kilómetros.

Radio ecuatorial: 6.378 km

Diámetro Polar: 12.713 kilómetros.

Radio polar: 6.356,5 km

Circunferencia que pasa por los polos: 40.013 km.

Circunferencia Ecuatorial: 40.076 kilómetros.

Masa: 5,972 x 10²⁴ kg
Superficie: 510.100.000 km²

Distancia media desde el Sol: 149.600.000 km.

Ahora, veamos un hito en las mediciones terrestres: la del arco de meridiano.

¿Qué es un arco de meridiano?

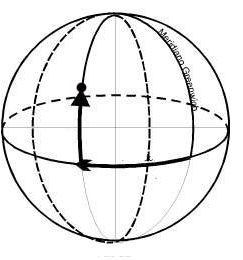
Figura 1.

Voy a adelantarme un poco a posts en los que hablaremos de meridianos, paralelos y otras yerbas, pero sepamos que un meridiano es una línea imaginaria, definida como un semicírculo máximo del globo terrestre que pasa por sus polos de rotación. Un arco de él es, obviamente, una distancia medida a lo largo de la superficie terrestre, pero siguiendo el recorrido ideal del meridiano del lugar. (Figura 1).

¿Para qué sirve conocer la longitud de un arco de meridiano?

Para conocer el perímetro total de la circunferencia a que dicho arco pertenece. Asumiendo a la Tierra como una esfera, podría asumirse también que la circunferencia que pasa por los polos y la ecuatorial son similares; y es así como se estableció por primera vez, en el S III a.C.

Pero veamos en un dibujito muy simple cómo es el razonamiento que nos permite deducir la circunferencia total, a partir de la medida longitudinal de un arco cualquiera. Para hacerlo más simple, lo que les esquematicé es un arco tendido por un ángulo de 90°, pero la línea argumental sería la misma con cualquier otro valor angular.

Figura 2

Vean la Figura 2, por favor. En ella, he marcado un ángulo AOB de 90°. Luego, pensando en que la circunferencia completa mide 360°, con sólo dividir 360 por 90, puedo saber cuántas veces se repite el ángulo en el circuito completo.

En un segundo análisis, recordemos que ese mismo cociente será el número de veces que también el arco se repite a lo largo de la circunferencia. En nuestro ejemplo, el número es 4, pero podemos generalizarlo dividiendo 360° por cualquier ángulo x que hayamos medido, y el valor de la longitud del arco correspondiente será el valor a, resultado de ese cociente.

Ahora supongamos que en nuestro ejemplo el arco es de 50 cm (no piensen en la Tierra ahora). Como el arco se repetía 4 veces (número a en cualquier otro caso) y como ángulos iguales subtienden arcos iguales, multiplicando 50 por 4, sé que la circunferencia en ese caso medía 200 cm.

Para universalizar el ejemplo, digamos que multiplicamos la longitud medida para el arco del ángulo x seleccionado, por el número a que son las veces que se repite ese arco.

Es así que llegamos fácilmente a la fórmula para el perímetro de la circunferencia.

Repitamos un poco: los datos son la longitud del arco y la cantidad de veces que se repite, que a su vez resulta de dividir 360° por el ángulo correspondiente que subtiende el arco elegido.

Perímetro de la circunferencia:

360°/ x (ángulo medido) x a (longitud medida) = resultado buscado, es decir el perímetro.

Tengan esto en la mente, porque lo mencionaremos en la segunda parte del post el lunes próximo.

¿Quién midió el arco de meridiano por primera vez?

El primer científico que intentó esta medición fue Eratóstenes de Cyrene, (Lybia) cuando era director de la legendaria Biblioteca de Alejandría.

¿Quién fue Eratóstenes?

Eratóstenes nació en el año 276 a.C. y murió en el 194 a. C. en Alejandría. Luego de estudiar en Atenas y Alejandría se destacó como astrónomo, matemático, historiador, geógrafo, filósofo y hasta poeta y crítico teatral .

Además del cálculo que hoy nos ocupa y que lo inmortalizó, estableció las distancias al Sol y a la Luna, midió casi con precisión la inclinación de la eclíptica en 23º 51′ 15″, y realizó un catálogo de cerca de 675 estrellas.

La riqueza de su vida es tal que alguna vez la comentaremos en un post ad hoc.

A partir de aquí, las siguientes preguntas pasan a la segunda parte de este post, que publicaré el próximo lunes:

¿Cómo se dio cuenta de que la Tierra era redonda y de que podía medir su circunferencia?

¿Cómo formuló la medición del arco de meridiano?

¿Qué valor obtuvo?

¿Cuál es el valor que hoy consideramos el más preciso para la circunferencia de la Tierra?

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La imagen que ilustra el post es de este sitio.

La figura 1 es de esta página.

2 comentarios para “Las dimensiones de la Tierra. Hoy Eratóstenes. Parte 1.”