Locos por la Geología

Para poder seguir avanzando en el reconocimiento de las medidas de nuestro planeta, es importante que repasen dos posts anteriores, o más propiamente dicho, un post en dos entregas.

En la primera parte, les expliqué la Ley de la Gravitación Universal, que será la base teórica de lo que analizaremos hoy, y sin la cual no entenderán nada. En la segunda, les adelanté una descripción muy general del experimento con que se «pesó» la Tierra, y que prometí aclarar en detalle más adelante, que es precisamente lo que me dispongo a hacer ahora.

¿Con qué datos se contaba antes de esta medición?

Como habrán visto en los posts que les mandé a leer, se tenía clara la fórmula de la gravedad universal, donde figuraba la Constante de la Gravedad, pero ésta era desconocida hasta la experiencia que hoy nos ocupa.

Por otra parte, ya desde muchos siglos antes se conocía la longitud del arco de meridiano, gracias a la determinación de Eratóstenes que les conté en este otro post .

Conocer la longitud del arco de meridiano permitió a su vez definir la circunferencia de la Tierra, según las inferencias que les mostré en la parte 1 del post que he linkeado más arriba.

Ahora bien, una vez que se conoce el perímetro de la circunferencia, sólo es cuestión de aplicar un par de fórmulas básicas y sencillas de la Geometría para obtener datos que necesitamos para «pesar» la Tierra.

Sabemos que el perímetro de la circunferencia (Pc) es:

Pc= π . d

donde π es pi, de valor conocido; y d es el diámetro (o dos veces el radio) de la Tierra, que buscamos conocer. Despejando pues en la fórmula, resulta:

d= Pc/ π

Y una vez que se ha calculado el radio r (que es la mitad del diámetro), sólo hay que usarlo en la fórmula del volumen de la esfera (Ve).

Ve= 4/3 π . r³

El volumen resultante al aplicar la fórmula con los valores del planeta, fue de 1,0842 x 10⁸ km³. Por supuesto que se trata de un volumen sólo aproximado, porque, como también les he explicado, la Tierra dista mucho de ser una simple pelota. Más bien se da el lujo de tener una forma propia a la que llamamos geoide, pero cuyo volumen podemos a través de esa fórmula medianamente estimar. Y todavía hacemos otra concesión, ya que en lo que sigue, pensaremos el volumen como equivalente a la masa, porque en cierta medida lo es.

Aδun con todas estas dispensas, ya contamos con una parte de los datos que requerimos para conocer la densidad (δ) de la Tierra. Como sabemos que densidad es el cociente entre la masa y el volumen, bastará con determinar la masa para conocer su densidad según la fórmula:

δ= M/V

donde δ es densidad; M es masa y V es volumen.

¿En qué consiste el experimento de Cavendish?

Ya les dije en uno de los posts que les mandé a leer, que el experimento con el que se pretendió «pesar la Tierra» fue ideado por Lord Cavendish en 1798, en su casa de Clapham Common. En los hechos, no fue la masa de la Tierra lo que determinó en realidad con ese experimento, sino el valor de la constante Universal de la Gravedad (G), pero una vez que se conoció ésta, el paso siguiente fue muy sencillo, y ya pudo conocerse el valor de la masa terrestre agregando sólo un datito más.

El punto de partida es la fórmula de F que es la fuerza de atracción gravitacional.

F= G. m.m’ / r²

Recordemos que F es la fuerza de atracción que se ejerce siempre entre dos cuerpos cualquiera.

m es la masa de uno de los cuerpos sometidos a esa fuerza.

m’ es la masa del otro cuerpo.

r es la distancia que separa ambos cuerpos.

Ahora veamos la construcción de la balanza de Cavendish, que es la que se ve en la ilustración superior. Este aparato consta de dos masas m y m’ , cada una de las cuales está a su vez dividida en dos esferas de plomo, pequeñas en el caso de m, y grandes en el caso de m’, pero todas de valor conocido.

Las dos bolas que forman la masa m están suspendidas de una estructura que al impedirles caer, las independiza de la atracción gravitacional terrestre, y las hace en cambio dependientes en su movimiento, sólo de la atracción gravitacional ejercida por las otras dos esferas que suman la masa m’. Éstas, a su vez, están sustentadas sobre un plato que les permite girar pero no caerse.

En definitiva, las esferitas solamente pueden girar alrededor de los ejes de los aparejos que las sostienen, y lo hacen en respuesta a la fuerza gravitatoria F que se genera entre ambas masas m y m’. Obviamente, esa fuerza responde a la fórmula general de la gravedad ya repasda más arriba.

Como los detalles de construcción del aparato son todos conocidos, se sabe de antemano cuál es el valor de las masas m y m’, y también el del radio r que las separa. Para conocer G, hay que medir F y resolver la ecuación, que ahora pasará a ser:

G= F. r² / m.m’

Cavendish resolvió el problema de manera sencilla: el cable del cual penden las esferas que constituyen la masa m tiene un módulo de torsión conocido, es decir que gira un cierto ángulo bien determinado por cada unidad de fuerza aplicada. Estableciendo cuánto ha rotado el hilo se mide pues F. Ésa es la función del espejo solidario con el cable, y que a medida que más se tuerce éste, va reflejando la luz incidente sobre él, en una porción más alejada de la inicial, que se toma como cero, en la escala graduada.

Con todos los valores ya conocidos, se pudo establecer la constante universal de la gravedad, en la cifra aiguiente:

G= 6,674 . 10¹¹ N . m²/ kg²  donde N es Newton, una unidad de medida de la fuerza, m es metro y kg , obviamente, kilogramo.

Ya se conoce, entonces el valor G, pero sigue en pie la incógnita relativa a la masa de la Tierra. Ése fue el paso siguiente.

¿Qué determinación siguió luego?

Ahora con la constante G medida, sólo se requiere reemplazar una de las masas del sistema de medición, por la masa de la Tierra misma. Ni pensar en colgarla del aparejo, de modo que simplemente, lo que se hace es permitir la acción de la gravedad terrestre, colgando una masa conocida m, de un resorte vertical, (Figura 1) que le permite «caer» tanto como sea atraída por la masa terrestre. El resorte tiene un módulo de deformación (por estiramiento) conocido, que representa la fuerza ejercida por la interacción de las masas m del explorador y M de la Tierra, y modificada por la distania que las separa. Otra vez la formulita.

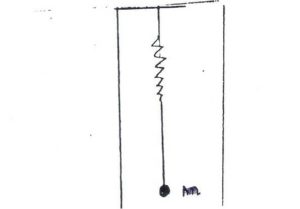
Figura 1.

En este caso, se conoce m de antemano, F se deduce del estiramiento del resorte, G, es constante y ya medida, y r es el radio de la Tierra, más la altura del punto del que pende la masa m. Resolviemdo la fórmula se midió por fin la masa de la Tierra.

¿Qué resultados se obtuvieron?

Las primeras mediciones estimaron una masa aproximada de unos 5.876 trillones de toneladas y una densidad de 5,48 g /cm³. Posteriormente, Poynting, en 1878, refinó un tanto la construcción del aparato, pero sólo logró una mínima corrección, estableciendo la densidad en 5,49 g /cm³.

¿Cómo evolucionó luego ese conocimiento?

Hubo numerosas correcciones desde entonces, que nunca se alejaron demasiado de los resultados arrojados por el experimento original. No fue sino hasta la segunda mitad del S XX, que se dieron a conocer valores más precisos, en función de los datos obtenidos a partir de los lanzamientos de satélites artificiales, cuando la observación de las desviaciones en sus trayectorias, por efectos de la gravedad terrestre, abrió un nuevo campo de experimentación. Los valores promedio que se aceptan hoy son de 5,98 . 10²⁷ g para la masa, y  5, 517 g /cm³ para la densidad.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La imagen que ilustra el post es de «Fundamentos de Geomorfología» de Rice, ligeramente modificada por mí.

2 comentarios para “Determinación de la masa y densidad de la Tierra”