Locos por la Geología

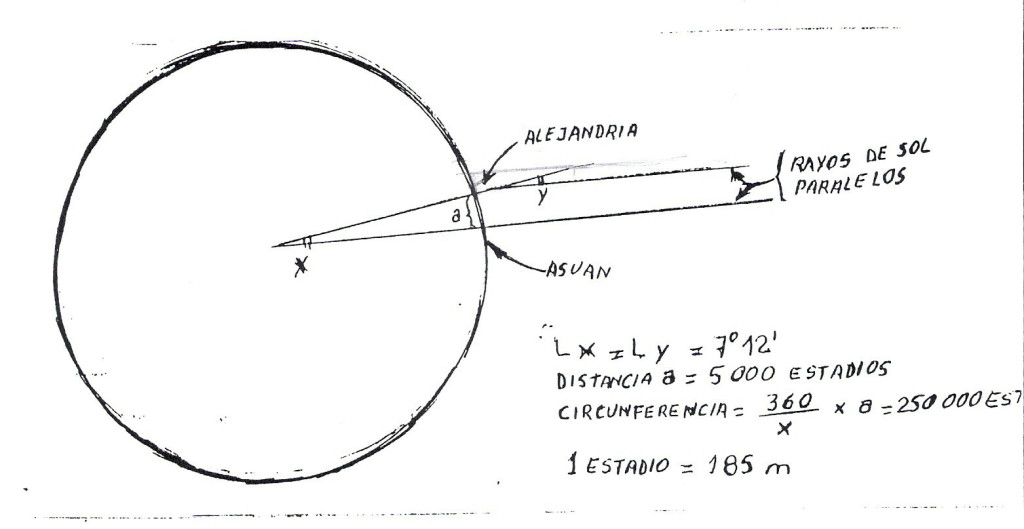
Figura 1

Este post es continuación del de la semana pasada, de modo que deberían empezar por leerlo antes de internarse en el de hoy.

El lunes pasado respondí las siguientes preguntas:

¿Cuáles son las dimensiones más significativas de la Tierra?

¿Qué es un arco de meridiano?

¿Para qué sirve conocer la longitud del arco de meridiano?

¿Quién midió el arco de meridiano por primera vez?

¿Quién fue Eratóstenes?

A partir de aquí, retomamos las preguntas que quedaron pendientes en la primera parte de este post, que publiqué el lunes pasado:

¿Cómo se dio cuenta de que la Tierra era redonda y que podpia medir su circunferencia?

En primer lugar, recordemos que los griegos ya sabían de la esfericidad de la Tierra desde el Siglo V antes de Cristo, en función de observaciones que ya les he comentado antes, pero en el caso particular de Eratóstenes, las pruebas de que se valió fueron relativamente sencillas.

Siendo director de la Biblioteca de Alejandría, Eratóstenes tenía acceso a información muy calificada para la época, y en uno de los tantos papiros en los que esa información se registraba, leyó que en la ciudad de Siena, (hoy llamada Assuán y situada unos 800 km al sureste de Alejandría) los rayos solares al caer sobre una vara el mediodía del solsticio de verano (el actual 21 de junio) no producían sombra alguna.

Picado por la curiosidad, Eratóstenes comenzó a replicar esas observaciones en Alejandría, utilizando la iluminación en un pozo, que era completa siempre en un mismo día y a la misma hora, y se desplazaba, en cambio, dejando parte del pozo en sombras en cualquier otro momento.

No obstante, las horas de sombra cero no coincidían en los registros de ambas ciudades. Ahora bien, asumiendo, muy correctamente que si el Sol se encuentra a una distancia tan grande que es comparativamente infinita respecto a las consignadas en la Tierra, sus rayos son paralelos, ya que se reúnen precisamente en el infinito.

El sabio coninuó un paso más adelante, razonando que si los rayos solares son paralelos, al alcanzar una Tierra plana, como algunos todavía insistían por entonces, no debería haber diferencias entre las sombras proyectadas por los objetos a la misma hora del mismo día, independientemente de la distancia entre ellos. Las diferencias en las sombras sólo podían explicarse sobre una superficie curva, tal como se ve en la Figura 2.

Con esos mismos juegos de distancias y sombras, midió el arco de meridiano que le serviría para establecer en seguida la circunferencia de la Tierra, tal como les expliqué el lunes pasado.

Figura 2

¿Cómo formuló la medición del arco de meridiano?

Con esas observaciones previas como dato inicial, Eratóstenes se valió del razonamiento que les muestro en la Figura 1, para medir el arco de meridiano (a en ese dibujo).

Como pueden ver en el diagrama, los rayos solares, considerados paralelos definen en Siena sombra cero para una estaca, pero en Alejandría, arrojan una sombra con una estaca (que al estar vertical sería como una continuación del radio terrestre), y forman con esa estaca un á¡ngulo ( denominado y en el dibujo), que resulta igual al ángulo interno de la Tierra (x del dibujo) que subtiende al arco a entre Siena y Alejandría, cuya longitud pretendía medir.

Los ángulos x e y son iguales, precisamente porque son ángulos correspondientes entre paralelas, y un teorema ya existente había demostrado ese postulado.

En definitiva, para conocer el valor de x, bastaba con medir y. Grande es la tentación de asumir que Eratóstenes se valió de la resolución trigonométrica del triángulo rectángulo entre los rayos, la estaca y su sombra…pero no. No se conocían los valores trigonométricos por entonces, de modo que utilizó un antiguo aparato denominado gnomon, y logró el valor de 7° 12′ para el ángulo y, exactamente igual a x.

Lo que siguió fue medir la distancia entre Siena y Alejandría, lo cual no se sabe exactamente cómo se realizó, tal vez contratando uno o más esclavos, como es la teoría más elegida; o encargando la cuenta a tropas que marchaban entre ambas ciudades, o a caravanas comerciales. Cualquiera haya sido el modo, Eratóstenes conoció también la distancia a, medida en estadios, como era lo normal en la época.

Con los valores de x y a ya en la bolsa, sólo tuvo que aplicar la fórmula que les puse en el dibujo, y que les expliqué la semana pasada, para conocer el perímetro de la cicunferencia terrestre.

¿Qué valor obtuvo?

Eratóstenes obtuvo un valor de aproximdamente 250.000 estadios, siendo la medida del estadio de 185 m. En definitiva, trasladando ese valor a las medidas actuales, el resultado es de 46.250 km.

¿Cuál es el valor que hoy consideramos el más preciso para la circunferencia de la Tierra?

Hoy se redondea y promedia el valor del perímetro de la circunferencia terrestre en 40.000 km, lo cual, si se considera la diferencia sideral entre los aparatos y métodos usados, asombra por su bajo error comparativo.

Como un plus más a la admiración que Eratóstenes nos provoca, es bueno recordar que él continuó por muchos años midiendo otros arcos de meridiano, y al encontrar variaciones significativas entre sus resultados, fue uno de los primeros en sugerir que la forma de la Tierra no era la de una esfera perfecta. En efecto, en una esfera perfecta, todos los ángulos iguales subtienden arcos iguales, cosa que no se reflejaba en sus calculos.

Para confirmar esta apreciación habrían de transcurrir por lo menos diecinueve siglos, pero eso ya es tema para otros posts.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

2 comentarios para “Las dimensiones de la Tierra. Hoy Eratóstenes. Parte 2.”