Locos por la Geología

Ya les he dicho muchas veces que para entender cosas como el cambio climático, no podemos desprendernos del entorno cósmico de nuestro planeta.

Por eso es que vengo lentamente avanzando con el conocimiento del universo primero, y ahora ya más metidos en el «barrio» en que vivimos, nos estamos adentrando en las características del Sistema Solar.

Les recomiendo pues que repasen los posts relativos a las leyes que rigen su dinámica, y también los más descriptivos, para comprender los elementos que lo constituyen.

¿Qué ley nos ocupa hoy?

La ley de Titius-Bode, que fue enunciada por el astrónomo Titius en 1776, y luego perfeccionada por Bode.

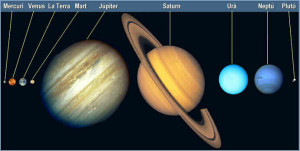
En ella se describe la distribución de los cuerpos celestes en el interior del Sistema Solar, lo que se logra a través de una relación matemática entre las respectivas distancias de los planetas al Sol. Dichas distancias se miden en «unidades astronómicas».

¿Qué es una unidad astronómica?

Una unidad astronómica (u.a.) es la distancia media del centro de la Tierra al centro del Sol. Y digo distancia media, porque si ustedes recuerdan las leyes de Kepler, que ya les recomendé repasar, las órbitas que describen los planetas alrededor del sol son elípticas, no circulares. Esto implica que hay un afelio y un perihelio a lo largo del año solar. El afelio es el momento de mayor alejamiento, y a la inversa, el perihelio es cuando la Tierra y el Sol más se aproximan.

Por esa razón, se habla de distancia promedio cuando se define la unidad astronómica.

¿Cómo se expresa matemáticamente la ley de Titius Bode?

La ecuación matemática que define- en unidades astronómicas «a»- la distancia entre cada planeta y el Sol, es:

a=0,4 + 0,3×2ⁿ ,  siendo n=1 para la Tierra.

Lo cual es obvio, porque a es precisamente la definición de la unidad astronómica, valiendo 1 para la Tierra, y como veremos más abajo, n también debe valer 1 para la Tierra si ha de cumplirse la relación matemática.

En definitiva, el patrón unitario es siempre relativo a nuestro propio planeta, porque después de todo, el ser humano siempre se considera a sí mismo como el centro de todo.

¿Cómo se aplica esta fórmula en cada caso?

Para Mercurio; n=1-2, ya que está dos lugares antes que la Tierra.

De allí surge:

a=0,4+ 0,3x 2 ^1-2 y siendo 2^-1  =½ , resulta

a =0,4+ 0,3x ½  es decir  a=0,4 +0,15= 0,55 u.a.

Y efectivamente, Mercurio se encuentra a muy poco más que la mitad de la distancia entre la tierra y el Sol.

Para Venus, a su vez;  n= 1-1=0,de donde

a= 0,4 + 0,3×2⁰  y siendo 2 ⁰ =1, resulta
a= 0,4 + 0,3 =0,7 u.a.
Y en efecto allí está Venus.

Para la Tierra:

a= 0,4 + 0,3×2 ¹  y ya que 2 ¹ =2,
a= 0,4 + 0,6  es decir  a= 1 u.a. Que por definición es la posición de la Tierra.

Para Marte:

a= 0,4 + 0,3×2 ¹⁺¹
a= 0,4 + 0,3×4= 0,4 + 1,2  y  a=1,6.

Siguiendo cálculos semejantes, se obtienen valores tales como 2,8; 5,2; 10; 19,6; 38,8; 77,2.

¿Se cumple esta ley en todos los casos?

Casi, porque todas estas distancias están en efecto ocupadas por planetas, salvo la correspondiente a 2,8 unidades astronómicas, que se halla «libre».

¿Qué consecuencias tuvo este descubrimiento?

Esta ley sugería la existencia de un planeta en la distancia de 2,8 u.a., predicción que fue confirmada en 1801 al descubrirse aproximadamente en esa posición, un pequeño cuerpo al que se denominó Ceres.

Luego se supo que Ceres no era el único cuerpo que orbitaba al Sol en esa región, sino que se trasladaban también allí, otros a los que se fue designando como Eros, Vesta, Palas, etc., a todos los cuales se llamó asteroides, y que se suponía formaban parte de un único planeta actualmente desintegrado, por causas que no se han dilucidado.

Conviene señalar que un gran número de investigadores creen en cambio, que estos asteroides son los restos de un planeta en embrión, cuya integración final fracasó por causas que tampoco aparecen claras.

¿Por qué significó un avance en el conocimiento del universo?

Porque conocer los sitios donde la probabilidad de encontrar un cuerpo era más alta, permitió un descubrimiento acelerado de los planetas y planetoides que se fueron sumando al inventario preexistente.

¿Tiene esta ley una explicación física?

Sí, efectivamente, la ley de la Gravedad define las distancias de equilbrio en que los cuerpos igualan sus atracciones mutuas, en función de sus respectivos volúmenes y densidades. Esta ecuación refleja las posiciones resultantes para un sistema cuya composición es precisamente la del Sistema Solar.

¿Es esta ley eterna e inmutable?

Las distancias entre los cuerpos del Sistema será siempre la que define la ley de Titius- Bode, salvo cambios de volúmenes o irrupciones de nuevos cuerpos.

Ambas cosas son posibles, ya que existe una cierta acreción de partículas cósmicas, y aproximaciones de cuerpos como los cometas o meteoritos, y hasta emisiones desde el cuerpo solar, que definen el dinamismo propio de los tiempos geológicos.

Un abrazo y hasta el miércoles. Graciela

Este post lo he construido sobre la base de un apunte de mi propia autoría que se identifica como sigue:

Argüello, Graciela L. 2006. «La Tierra como planeta integrante del Sistema Solar» Cuadernillo didáctico Nº II, Capítulo 1. Para circulación interna en la U.N.R.C. 17 páginas.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente, porque esta página está registrada con IBSN 04-10-1952-01. 

P.S.: La imagen que ilustra el post procede de este sitio.